
Performing Hohmann Transfers to Study the Sun
Ishaan Patel
University of Colorado - Boulder

Abstract
The Aditya-L1 mission seeks to send a spacecraft to the L1 Lagrange point in hopes of taking measurements from the Sun. In the presented study a hypothetical extension is proposed to map projections of Earth, Venus, and Mercury about the Sun via basic two body orbital mechanics. In addition, general interplanetary mission design concepts are demonstrated to depict potential Hohmann transits from Earth to Venus and from Venus to Mercury. The overall results conclude that such an extension is feasible, though not very likely due to the drawbacks of a implementing such a large total change in velocity for the maneuvers.

Introduction
POSSIBILITY
If the primary purpose of the Aditya-L1 mission is to study the Sun, then it would be logical to assume that having data corresponding to multiple parts of the Sun would be even more beneficial. This could be done by perhaps sending a spacecraft to different Lagrange points such as L3, L4, or L5. However, after aimlessly browsing through a simulation of planetary trajectories, it became clear that Earth, Venus, Mercury would be surprisingly close in alignment around April of 2017 [4].

IDEA
Aditya-L1 is the first mission by the Indian Space Research Organisation (ISRO) to study the Sun. Its purpose is to observe and take measurements in order to better understand the processes that affect the solar corona and accelerate the solar wind. The satellite itself, consisting of six equipment payloads [5], is set to be placed in a halo orbit around the L1 Lagrange point sometime in 2019 or 2020. Its coronagraph and ultraviolet (UV) imager will hope provide observations of Sun's Protosphere and Chromosphere, respectively [2].
Figure 1: Lagrange Points [3]

APPROACH
Instead of attempting to stabilize a spacecraft at a Lagrange point, why not send a spacecraft to Venus? Such an opportunity will not arise again for several decades. However, the time frame for this mission boldly dictates the lack of feasibility for this idea. The analysis presented assumes that the Aditya-L1 mission had already been conceived prior to 2015, and that the spacecraft was capable of performing large change in velocities (and other necessary maneuvers).


Concepts
General Assumptions
For this analysis, several assumptions will be made. First, each object in space is treated as a point mass for simplicity and to apply the equations of motion for the "two-body" problem (Eq. 1).
(1)
It is also assumed that the objects in consideration for this analysis are revolving in circular orbits around the Sun, which is stationary. Furthermore, perturbations such as solar radiation, atmospheric drag, and the gravity of nearby objects during transit are neglected as this study generalizes this scenario via the "Vis-Viva" equation and its corresponding derivations. The maneuvers utilized in this study also assume that the transit is coplanar. Lastly, the mass of the Sun is much greater than the mass of any planet in our solar system; and likewise, the mass of any planet is much greater than any spacecraft to date. Then for the final assumption it is valid to say that when dealing with a spacecraft moving locally about a planet, the mass of the planet -- and in turn, its gravity -- will have a greater influence on the spacecraft than the spacecraft will have on the planet. Similarly, when dealing with celestial objects within our solar system, it is logical to state that the Sun will have a greater influence on the planets than the planets will have on the Sun [10].
Spheres of Influence
Continuing on with the gravity (or force) of an object on another, an important concept to consider for this analysis is the sphere of influence (SOI) of an object. According to Vallado, a body's SOI is considered to be the "region of space within which the motion of a particle is influenced by that object's gravity more than any other perturbing body." After further simplification of the Eq. 1, Vallado shows that the radius of an object's sphere of influence with respect to a central body can be shown by Eq. 2 below.
(2)
In a sense, one can visualize spheres of influence as being literal "spheres" around an object in space. If a smaller object such as an asteroid, space debris, or even a spacecraft were to enter this sphere around a certain object, then that object's gravitational force becomes its primary natural influence in motion [10].
The Interplanetary Mission
The proposed hypothetical mission for this analysis begins in a circular orbit about Earth. The spacecraft would then perform a Hohmann transfer to Venus. From Venus, one of two situations can take place. First, the spacecraft could continue to maintain an orbit around Venus so that it could collect measurements from the Sun taken at a different viewpoint other than Earth. The second situation depicts a scenario where the spacecraft could separate into two. This would be to allow the primary spacecraft to continue to orbit around Venus while the secondary spacecraft would perform another Hohmann transfer to Mercury. Note that during this same time period, Mercury is also at a very close approach to Venus. This analysis considers the second scenario to provide provide projections of planets with respect to the Sun as well as a simulation for both of the aforementioned Hohmann transfers.
Hohmann Transfer Concepts
To better understand how the transfers to Venus and Mercury will be simulated, first consider the concepts of Hohmann transfers in general. For the initial case, the spacecraft will be in a circular orbit around the Earth at an altitude of 200 km. After the spacecraft performs the transfer, it will have to enter a circular orbit around Venus at an altitude of 200 km. Similarly, the spacecraft will enter a circular orbit at an altitude of 200 km as it arrives Mercury. However, the spacecraft will have to perform two maneuvers requiring two change in velocities (ΔV) for the transfer to take place. This is because once the spacecraft arrives at its targeted planet, it will have to readjust its velocity to properly align with the velocity of the planet. Equation 3 can be used to compute the velocities of each respective planet (assuming a circular orbit around its corresponding major body).
(3)
The next step is to compute the transfer orbit parameters such as the semimajor axis (a) and the eccentricity (e). This can be done via the formulas in Eq. 4.
(4)
These values can then be used to compute the velocities at the transfer orbit periapsis and apoapsis given by Eq. 5 below. Note that these velocities are not the same when referring to the planet or spacecraft's Heliocentric velocity. When referring to the velocity with respect to the Sun, one must add the velocity vector the the velocity vector o the planet because the local velocity differs from the velocity of the spacecraft combined with the movement of of the planet about the Sun.
(5)
Finally, to compute the ΔV necessary in order to perform a Hohmann transfer Eq. 6 can be applied for the maneuver from Earth to Venus. Likewise, the ΔVs necessary for the trip from Venus to Mercury can be computed as well.
(6)
Note that the other general Keplerian orbit parameters used in this analysis were computed using the formulas provided by Dr. Nerem of the University of Colorado - Boulder, as well as the literature by Vallado [10].
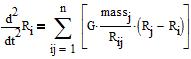
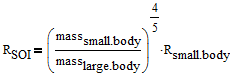



Extension
Plotting Trajectories
This extension was proposed on the basis that such a mission would be ideal in the very near future due to the fact that the planets Earth, Venus, and Mercury will be in very close proximity to each other. To test and visualize this scenario, the trajectories of the three planets were plotted with respect to the Sun. Thus, the majority of the parameters used to do so were adjusted accordingly. For example, it would be as if the planets were treated as "satellites" while the Sun would be treated as a "planet" in terms of gravitational force.
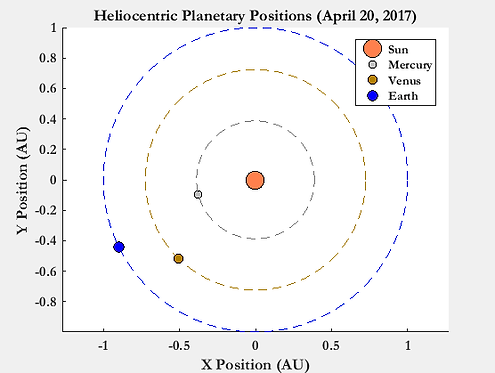
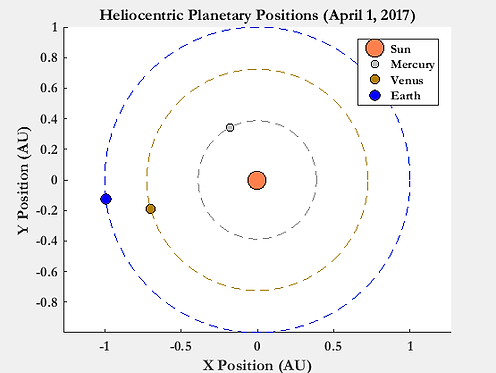
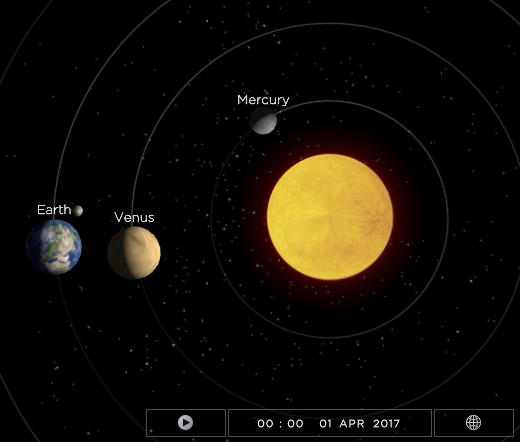
General computations such as the period, mean anomaly, and mean motion were found. As a reference date, October 1, 2016 at 00:00:00 MST was chosen. This was the date that the reference ephemeris files were generated via the Jet Propulsion Laboratory HORIZONS database [6]. Ideally, generating the file closer to the time period being analyzed would provide more accurate depictions of the planets' trajectories. As predicted a priori, Earth, Venus, and Mercury do in fact align at close proximity with one another near late March and April of 2017 (seen in Fig. 2 below). Note that the position is portrayed in terms of astronomical units (AU) for plot and visual aesthetics. To check the validity of this portrayal (Fig. 3), an online simulation via SolarSystemScope was utilized [4]; as can be seen, the simulation via the ephemeris file is deemed logical.
Figure 2: Calculated Position of Planets around Sun
Figure 3: Projected Positions as per SolarSystemScope [4]
The First Transfer
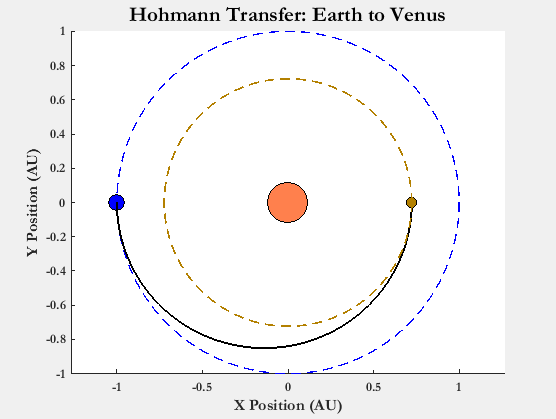
The initial Hohmann transfer that the spacecraft would have to perform is from Earth to Venus. Using the equations in the previous section, it was calculated that a total ΔV of approximately 65 km/s is needed to perform the first transfer. The ΔV upon departing Earth would have to be a -27.2 km/s and the ΔV upon arriving at Venus would have to be around 37.7 km/s. At first glance, this seems valid because in order to get to the outer planets such as Jupiter or even Mars, a spacecraft would have to gain ΔV to rendezvous with the object. However, for the inner planets such as Venus and Mercury, a spacecraft would have to lose ΔV with respect to the Sun. These values do seem relatively high for such a maneuver, however it is important to note that the spacecraft itself has been assumed to be capable of performing such feats. Figure 4 below shows what the potential first Hohmann transfer would look like. It has also been estimated that the time it would take to do the maneuver is approximately 146 days. Now this value is fairly reasonable considering that the Mariner was able to reach Venus in approximately 100 days. So, the spacecraft in the proposed extension would have had to be launched on November 6, 2016, in order to have reached Venus around April 1st of the following year [9].
Figure 4
The Second Transfer
The next Hohmann transfer is between Venus and Mercury. Figure 4 depicts this transfer with respect to the Sun. It is important to note that in both Figs. 4 and 5, the depiction of Venus and Mercury, respectively, is the final position of that planet - not the position when the spacecraft initially departs the primary object. For this second transfer, the initial ΔV is -29.2 km/s and the arrival ΔV is 54.6 km/s. Thus, the total ΔV for this maneuver is approximately 84 km/s. In addition, this performance would take an over time of roughly 75 days; that is, the secondary spacecraft would reach Mercury around May 10, 2017 (on Earth) [9].
Figure 5
Reflections on Planetary Positions
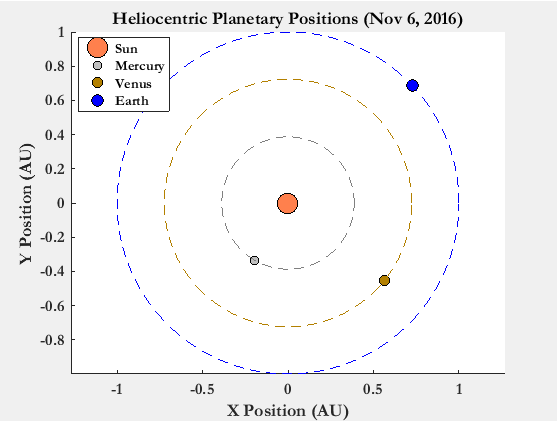
The above visuals are ideal for depicting the Hohmann transfers between the planets. However, in order to get a better understanding of where the planets are on the aforementioned dates of arrival, consider Fig. 6. It depicts the position of Earth, Venus, and Mercury around the Sun when the proposed spacecraft departs Earth in transit to arrive at Venus on April 1, 2017, as depicted in Fig. 2.
Figure 6
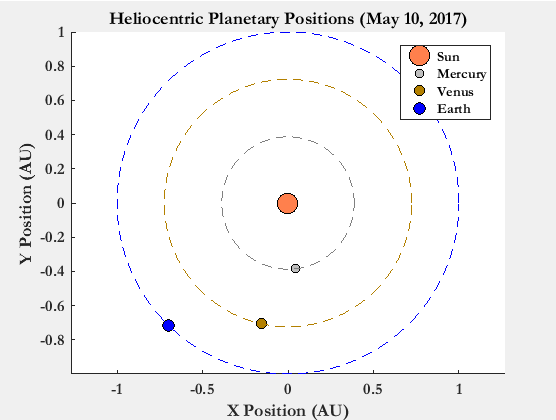
Finally, Fig. 7 shows the positions of the planets when the secondary spacecraft finally arrives at Mercury in May.
Figure 7


Conclusion
The extension demonstrated in this study utilized various fundamentals of orbital mechanics and interplanetary mission design in order to project the position of planets around the Sun at a certain date from a reference point. This was used in conjunction with some patched conics concepts such as spheres of influence in order to perform two uniquely possible Hohmann transfers (assuming the capabilities for such maneuvers existed on contemporary spacecraft). Numerous other assumptions were made in order to perform other two-body calculations; thus, the projections provided in this analysis are merely rough estimates. The computations provide a theoretical possibility of sending a spacecraft from Earth to Venus, where it would then separate to send a secondary spacecraft to Mercury. These two spacecraft could then potentially obtain measurements from the Sun at different locations and times, rather than from solely one viewpoint as is planned for the Aditya-L1 mission by ISRO.
From the results presented in this analysis it is clear that performing such a mission requires large amounts of ΔV, especially as a spacecraft executes a Hohmann transfer to a planet closer to the Sun. For the case with Mercury, there have only been two spacecraft to date to have even come close to Mercury: the Mariner 10 and the Messenger. This is because such a high ΔV to get to Mercury from Venus is about as much ΔV it would in order to reach Jupiter from Earth (via gravity assists, of course). Therefore, such a task is feasible, though not entirely ideal with today's technology in space exploration.
Future tasks related to this study could possibly aim to perform a flyby of Venus and Mercury, respectively, in order to minimize the total ΔV. This would be done by using gravity assists from the planet as it revolves about the Sun. Mariner 10 was able to perform a flyby of Mercury, but it is important to note that this was a much smaller spacecraft than what would be in consideration for the proposed extension. In addition, getting Messenger into an orbit around Mercury required numerous gravity assists for the mission to be practical as well [8]. Apart from the trajectory, it would be useful to map out when and at what locations about the Sun the spacecraft on Mercury would be in a line of sight with the craft on Venus or a ground station on Earth; and similarly, a projection of when the spacecraft on Venus would have a line of sight with a ground station on Earth would be an extremely useful future analysis related to this project.

